Lógica Matemática

Lógica Matemática

Lógica Proposicional 

• La lógica proposicional o lógica de orden cero es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas lógicas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.
• La lógica proposicional o lógica de orden cero es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas lógicas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.

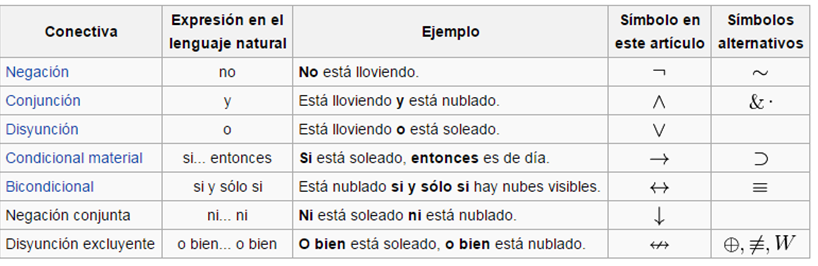
Ejemplos:

1. Mañana es miércoles o mañana es jueves.
2. Mañana no es jueves.
3. Por lo tanto, mañana es miércoles.

Sin embargo, a pesar de que el argumento sea válido, esto no quiere decir que la conclusión sea verdadera. En otras palabras, si las premisas son falsas, entonces la conclusión también podría serlo. Pero si las premisas son verdaderas, entonces la conclusión también lo es. La validez del argumento no depende del significado de las expresiones «mañana es miércoles» ni «mañana es jueves», sino de la estructura misma del argumento. Estas premisas podrían cambiarse por otras y el argumento permanece válido. Por ejemplo:

1. Hoy está soleado o está nublado.
2. Hoy no está nublado.
3. Por lo tanto, hoy está soleado.

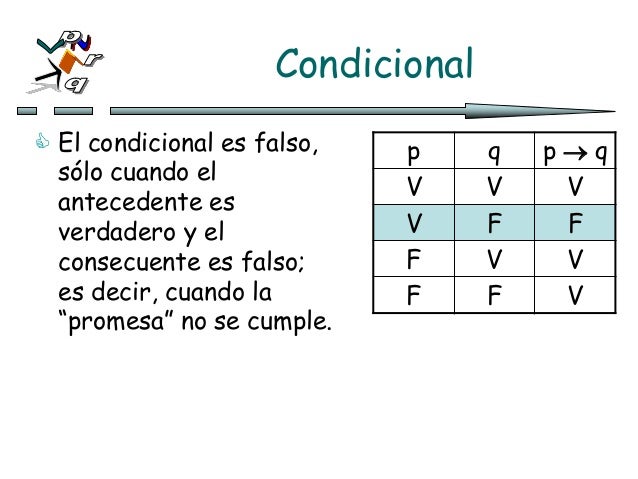
También tenemos que tener en cuenta El significado de las conectivas lógicas no es nada más que su comportamiento como funciones de verdad. Cada conectiva lógica se distingue de las otras por los valores de verdad que devuelve frente a las distintas combinaciones de valores de verdad que puede recibir. Esto quiere decir que el significado de cada conectiva lógica puede ilustrarse mediante una tabla que despliega los valores de verdad.

Clases De Proposiciones 

Las proposiciones forman parte de la forma más simple o elemental de la lógica, y se puede enfocar en la lógica matemática. Esta lógica, no profundiza en los conceptos de las proposiciones, sólo se guía en lo ciertas o falsas que sean.

Se le ha denominado como “Lógica de las proposiciones sin analizar” y se puede catalogar como una lógica superficial.

Ejemplos de una proposición simple : 

1. Un caballo negro
2. El esta dormido
3. Mi computadora
4. Un dia nublado 
5. Usas zapato
6. Lava su ropa 
7. Vamos a comer 
8. Salio el sol

Ejemplos de una proposiciòn compuesta 

El frijol es amarillo o negro 

El está componiendo coches o bicicleta 

La computadora es grande pequeña 

Su teléfono es negro o rosa

Propiedades de los operadores logicos

Los operadores definidas entre las formas proposicionales y algunas de sus más importantes propiedades se incluye en las denominadas leyes algebraicas de proposiciones  leyes lógicas.
  

idempotencia:La idempotencia es la propiedad para realizar una acción determinada varias veces y aun así conseguir el mismo resultado que se obtendría si se realizase una sola vez.

Por ejemplo, los dos únicos números reales que son idempotentes, para la operación producto (•), son 0 y 1. (0•0=0,1•1=1).

Asociatividad:La asociatividad es una propiedad en el álgebra y la lógica proposicional que se cumple si, dados tres o más elementos cualquiera de un conjunto determinado, se verifica que existe una operación: , que cumpla la igualdad:

Conmutativa:

En matemáticas, la propiedad conmutativa o conmutatividad es una propiedad fundamental que tienen algunas operaciones según la cual el resultado de operar dos elementos no depende del orden en que se toman. Esto se cumple en la adición y la multiplicación ordinarias

Distributiva:En matemáticas y en particular en álgebra abstracta, la distributiva es la propiedad de los operadores binarios que generaliza la propiedad distributiva del álgebra elemental.

La propiedad distributiva de la multiplicación sobre la suma en álgebra elemental es aquella en la que el resultado de un número multiplicado por la suma de dos o más sumandos, es igual a la suma de los productos de cada sumando por ese número. En términos algebraicos:

Identidad:En matemáticas, una identidad es la constatación de que dos objetos que matemáticamente se escriben diferente, son de hecho el mismo objeto.¹ En particular, una identidad es a una igualdad entre dos expresiones, lo que es cierto sean cuales sean los valores de las distintas variables empleadas.

Razonamiento

Un razonamiento lógico, en definitiva, es un proceso mental que implica la aplicación de la lógica. A partir de esta clase de razonamiento, se puede partir de una o de varias premisas para arribar a una conclusión que puede determinarse como verdadera, falsa o posible.

UNIDAD 2 CONJUNTOS

Definiciòn, tipo, cardinalidad 

Con el ánimo de evitar confusiones, cuando definimos un conjunto debemos especificar de donde se están tomando los elementos que lo conforman.  Esto significa que debe existir una base de la cual tomamos los elementos, esta base sobre el cual trabajamos es llamada conjunto universal.  Usaremos siempre la letra 

$U$

 para representar el conjunto universal.

Conjunto vacío: Para representar dicho conjunto usamos el conocido símbolo del vacío, como se muestra en la imagen de la derecha.

También, haciendo uso de la descripción por extensión, representamos el conjunto vacío por medio de los corchetes {}.    Como el conjunto vacío no tiene elementos, no podemos ubicar ningún elemento en el interior de los corchetes.

               

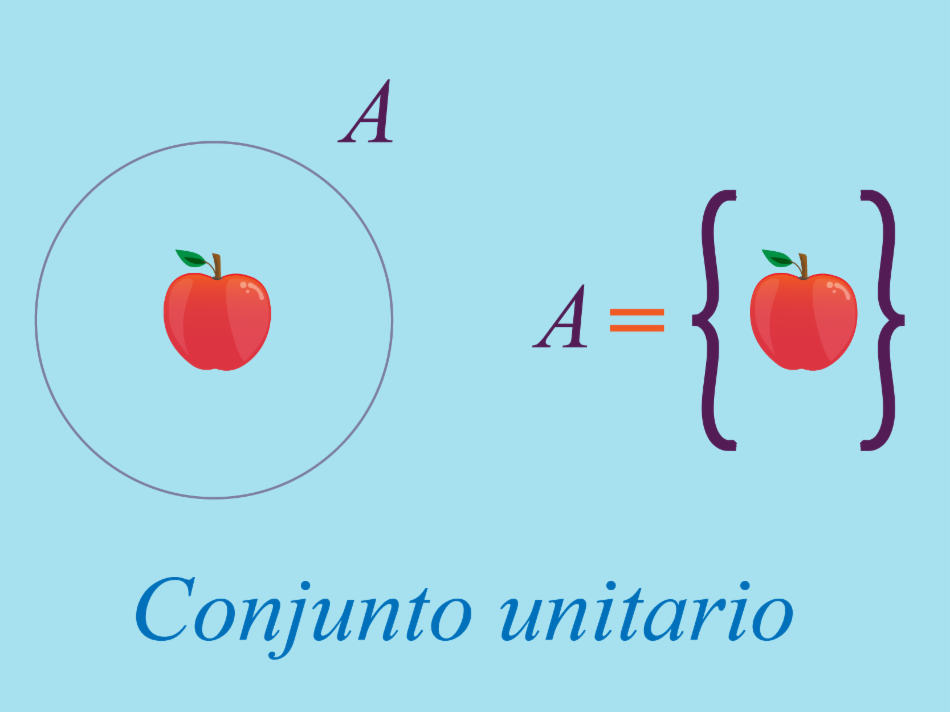
Conjunto Unitario:El conjunto unitario se distingue por tener solo un elemento.  No importa qué tipo de elemento tenga el conjunto, un gato, un perro, un número, una letra, o cualquier otra cosa, si tiene un solo elemento es llamado conjunto unitario.

Conjunto finito:Este tipo de conjunto también se distingue por la cantidad de elementos que posee.  Un conjunto es finito si podemos contar la cantidad de elementos que lo conforman.

Por ejemplo, el conjunto de las letras del idioma castellano es finito porque en total son 27 letras.  En la imagen de la derecha se muestran otros conjuntos finitos.  Te puedes dar cuenta que los conjuntos unitarios también son finitos

Conjunto infinito:No es fácil encontrar en la naturaleza ejemplos de este tipo de conjuntos.  Los conjuntos infinitos son aquellos a los cuales no les podemos contar la cantidad de elementos que los componen.  El método más fácil para representar este tipo de conjuntos es por comprensión.  Basta con mencionar las características que tienen en común los elementos del conjunto y los estaremos determinando a todos.  Considera el conjunto de los números que terminan en tres, podríamos definirlo así:  Sea 

$T=\{x\mid xesnúmeroyterminaentres\}$

Definición de Cuantificadores

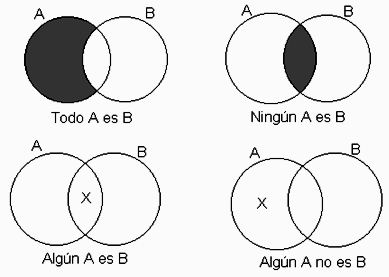
A instancias de la lógica, de las matemáticas y de la teoría de conjuntos, los cuantificadores son símbolos que se emplean en los mencionados contextos para poder señalar cuantos o los tipos de elementos que integran un conjunto dado y que cumplen con determinada propiedad.

Nos podremos encontrar con una variedad de cuantificadores, aunque, entre los más empleados se cuentan: cuantificador universal y cuantificador existencial.

Operaciones entre conjuntos

Además de relacionar los conjuntos a través de la contenencia y la igualdad, podemos crear unos nuevos a través de las operaciones entre conjuntos.  Aquí aprenderás de que se trata.

UNIÒN DE CONJUNTOS

Supongamos que tenemos los conjuntos $M$ y $N$ definidos como se muestra en la siguiente figura:

Podemos crear otro conjunto conformado con los elementos que pertenezcan a $M$ oa $N$.  A este nuevo conjunto le llamamos unión de $M$ y $N$, y lo notamos de la siguiente manera: $M\cup N$.  En la imagen de abajo puedes observar el resultado de unir los conjuntos $M$ y $N$.

INTERSECCIÓN DE CONJUNTOS

Sigamos tomando como ejemplo los conjuntos $M$ y $N$ definidos anteriormente.  Podemos determinar un nuevo conjunto conformado por los elementos que nuestros conjuntos $M$ y $N$ tienen en común.  A este nuevo conjunto le llamamos intersección de $M$ y $N$ y lo notamos de la siguiente manera: $M\cap N$.

DIFERENCIA DE  CONJUNTOS

En este caso se deben seleccionar los elementos de un conjunto que no estén en el otro.  Por ejemplo, si realizas la operación $M$ menos $N$, debes seleccionar los elementos de $M$ que no están en $N$.  Representamos la diferencia M menos N así: $M\backslash N$.  Observa que en este caso $M\backslash N=\{a,c\}$.

DIFERENCIA SIMETRICA DE CONJUNTOS

En esta ocasión se deben escoger los elementos de $M$ que no están en $N$, y los elementos de $N$ que no están en $M$.  Puedes ver el resultado de la diferencia simétrica entre $M$ y $N$ en la figura de la izquierda.  Representamos la diferencia simétrica a través del símbolo $\Delta$.  En el caso de nuestros conjuntos $M$ y $N$tenemos: $M\Delta N=\{a,c,g,1,e\}$.

PROPIEDADES DE LAS OPERACIONES DE CONJUNTOS

ASOCIATIVA:La suma tiene la propiedad asociativa y vamos a ver porqué.

Cuales quiera que sean los números a, b  y c, siempre se cumple la siguiente igualdad:

(a + b) + c = a + (b + c) = (a + c) + b

Fijaros en el siguiente ejemplo con números concretos.

Supongamos que a=3, b= 18 y c=1. Ya sabéis que primero hay que calcular los paréntesis.

(3 + 18) + 1 = 21 + 1 = 22

3 + (18 + 1) = 3 + 19  = 22

(3 + 1) + 18 = 4 + 18 = 22

• Propiedad conmutativa: El orden de los factores no varía el producto.

Vamos a ver un ejemplo de la propiedad conmutativa.

El resultado de multiplicar 10 x 3 será igual que al multiplicar 3 x 10. Aunque cambiemos el orden de los factores el resultado seguirá siendo 30.

• Elemento neutro: El 1 es el elemento neutro de la multiplicación porque todo número multiplicado por él da el mismo número.

En el ejemplo que os mostramos en la imagen, vemos que si multiplicamos 5 o 7 por la unidad, nos da como resultado 5 o 7. Por lo tanto cualquier número que multipliquemos por 1, nos dará como resultado el mismo número.

• Propiedad distributiva: La multiplicación de un número por una suma es igual a la suma de las multiplicaciones de dicho número por cada uno de los sumandos.

Pongamos un ejemplo: 2 x (3 + 5)

Según la propiedad distributiva 2 x (3 + 5) será igual a 2 x 3 + 2 x 5

Comprobemos si esto es cierto.

2 x (3 + 5) = 2 x 8 = 16

2 x 3 + 2 x 5 = 6 + 10 = 16

Ambas nos dan como resultado 16, por lo que queda demostrada la propiedad distributiva de la multiplicación.

Leyes de Morgan. Declarar que la suma de n variables preposicionales globalmente negadas (o invertidas) es igual al producto de las n variables negadas individualmente y que inversamente, el producto de n variables proposicionales globalmente negadas es igual a la suma de las n variables negadas individualmente. Demostración formal si y solo si y . para cualquier x: ó Por lo tanto inclusión: ó Con proposiciones. La prueba utiliza la asociatividad y la distributividad de las leyes y . Verdad Si verdad por n.

FUNCIÒN:En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera depende del valor de la segunda. Por ejemplo el área Ade un círculo es función de su radio r (el valor del área es proporcional al cuadrado del radio, A = π·r²). Del mismo modo, la duración T de un viaje en tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que se desplace el tren (la duración es inversamente proporcional a la velocidad, d / v). A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.

UNIDAD 3 NÚMEROS REALES  

NÚMEROS NATURALES:La exigencia y oportunidad de contar derivó necesariamente en la invención y el uso de los llamados actualmente números naturales. Aparecen en una gama de sistemas de numeración, en principio de carácter oral. Son los números más simples de los que hacemos uso, el conjunto de ellos se denota por . Entre estos números, en sucesión ascendente en representación indo-arábiga, son : 1,2,3,4,5... Se denominan también números enteros positivos.

NÚMEROS ENTEROS:

La insuficiencia de los números naturales para contar deudas o temperaturas por debajo de cero lleva directamente a los números enteros. Se denotan por  y estan formados por los números naturales, sus inversos aditivos y el cero. El conjunto de los números enteros incluye a los naturales, .

.

NÙMEROS IRRACIONALES:

La insuficiencia de los racionales al intentar encontrar la medida exacta de la diagonal de un triángulo rectángulo con catetos de longitud 1 lleva a los números irracionales. Se denotan por A veces se denota por  al conjunto de los números irracionales. Esta notación no es universal y muchos matemáticos la rechazan. Las razones son que el conjunto de números irracionales no constituyen ninguna estructura algebraica, como sí lo son los naturales (), los enteros (), los racionales (), los reales () y los complejos (), por un lado, y que la  es tan apropiada para designar al conjunto de números irracionales como al conjunto de números imaginarios

OPERACIONES CON NÚMEROS REALES 

En la adición de números reales, los términos que intervienen son los sumandos y el resultado, donde el orden de los sumandos no altera el resultado.

a+b=b+a$$a+b=b+a$$

al ser, los números reales, un conjunto que incluye los números negativos, la suma de negativos es posible, sin tener que recurrir a otro conjunto de números. Entonces, las sumas se pueden realizar como:

a+(−b)=(−b)+a=−b+a$$a+(-b)=(-b)+a=-b+a$$

Por ejemplo, podemos tomar los dos sumandos, 7$7$  y −11$-11$. El orden de estos, al sumarlos, no va a alterar el resultado, ya que se trata al sumando como un término en su valor absoluto. Pero si se lo tomara por su valor relativo, no se podría sumar 7+11 o 11+7 y esperar el mismo resultado que:

7+(−11)=−11+7=−4$$7+(-11)=-11+7=-4$$

En este caso, el resultado es negativo, ya que el sumando con valor negativo es mayor que el término con valor positivo.

EXPRESIONES ALGEBRAICA

una expresiòn algebraica es una expresiòn en la que se relacionan valores indeterminados con constantes y cifras  todos ellos ligados pr un numero finito de operaciones de suma, resta, producto, cociente, potencia y raiz.

expresiones algebraicas racionales

esas "fracciones que tienen polinomios en el numerador y denominador". 

Recuerda que una expresión algebraica es aquella formada por números y letras.

Una expresión algebraica es racional si su parte literal (es decir las letras) no está afectada por un radical.  (En caso de estar afectada la parte literal por un radical, será una expresión algebraica irracional).

Aprenderemos a trabajar con ellas: simplificarlas y realizar diversas operaciones (sumas, restas, multiplicaciones, divisiones)

                    A 

Expresiones algebraicas irracionales

Las expresiones algebraicas irracionales tienen algunas de sus variables bajo un signo radical o con exponente racional no entero.

Polinomios 

Polinomio Un polinomio es la suma de dos o más monomios. El grado de un polinomio es el grado del monomio de mayor grado que participa en él.

 Casos particulares Binomio: Es el polinomio formado por la suma algebraica de dos monomios

 Trinomio: Es aquel que es la suma algebraica de tres monomios Cuatrinomio

: Es el polinomio formado por cuatro monomios

RAZÓN:

Una razón indica en forma de división la relación entre dos cantidades. Nos indica cuántas unidades hay en relación a las otras, y se suele indicar simplificando las fracciones.

Por ejemplo, si en un salón de clases tenemos 24 niñas y 18 niños, entonces lo representaremos de alguna de las siguientes formas:

24/18
24:18

Y como la fracción podemos simplificarla al dividirla entre 6, entonces tendremos:

4/3
4:3

Y se lee que existe una razón de 4 a 3, o de 4 por cada 3.

Cada uno de los valores de una razón tiene un nombre. El valor que está del lado izquierdo de la relación, se le llama antecedente, y al valor del lado derecho se le llama consecuente.

PROPOSICIÓN:

La proporción indica mediante una igualdad la comparación de dos razones. Para escribir una proporción, debemos tener en cuenta que los valores antecedentes, siempre estén del mismo lado, al igual que los consecuentes.

En nuestro ejemplo del salón de clases, podemos comparar la razón que tenemos, de 4 niñas por cada 3 niños, y podremos calcular cuántos niños hay en un salón en relación al número de niñas o viceversa. Para esto, en primer lugar escribiremos la proporción que ya conocemos:

4:3

Después, un signo de igualdad

4:3=

Y después la cantidad total, por ejemplo la del mismo salón, recordando que debemos respetar el orden del antecedente y del consecuente. En nuestro ejemplo, el antecedente será el número de niñas, y el consecuente el número de niños.

4:3=24:18

ECUACIONES E INECUACIONES 

Las ecuaciones son expresiones algebraicas que incluyen una igualdad (=). Como seguro que recordáis, las expresiones algebraicas son aquellas que se componen de datos (números) e incógnitas (que puede ser x, ó y, ó…).

Las ecuaciones incluyen la igualdad mencionada antes porque es una herramienta que sirve para comparar. Realmente cuando resolvemos una ecuación estamos haciendo (sin ser conscientes muchas veces) la pregunta “¿Qué punto ó puntos tienen en común la expresión que está a la izquierda de la igualdad con la expresión que está a la derecha de la igualdad?”

Hay múltiples tipos de ecuaciones: de primer grado, de segundo grado, de grado n, logarítmicas, trigonométricas, exponenciales, sistemas de ecuaciones…

Lo importante en este caso es que quede muy claro que con las ecuaciones hallamos puntos, desde uno en los casos más fáciles, hasta infinitos puntos, pasando por el caso en el que no hay solución y por tanto no existe ningún punto que la cumpla.

Por otra parte tenemos las inecuaciones, que las podemos definir como una expresión algebraica que incluye una desigualdad. Recordemos que las desigualdades son:

• ≥ : Mayor o igual
• > : Mayor estrictamente
• ≤ : Menor o igual
• < : Menor estrictamente

Pues bien, la diferencia más esencial entre ecuaciones e inecuaciones, es que mientras que las ecuaciones calculan puntos como hemos dicho antes, las inecuaciones calculan semiplanos (o lo que es lo mismo, trozos de plano).

Por ejemplo, recordando que estamos hablando de inecuaciones en un plano, si tenemos como resultado x<0, lo tenemos que interpretar como todos los puntos (x,y) del plano cuya x sea negativa. Si nos fijamos, todos esos puntos juntos formarían el semiplano izquierdo, es decir, el trozo de plano completo que queda a la izquierda del eje y.

Fijaos que ha sido importante recalcar lo de que estamos trabajando en un plano, porque así el resultado es un semiplano. Si por ejemplo hubiéramos estado trabajando en una recta, el caso x<0 su resultado sería una semirrecta, porque los valores de x que lo cumplirían serían x=-1, x=-2, x=-3, x=-1’2, x=-1’27…

El cálculo de inecuaciones es muy similar al de ecuaciones. Tan solo hay que tener cuidado con los posibles cambios de desigualdad y, dado el caso en el que sea necesario, discutir los intervalos de puntos que son solución y los que no lo son.

Siempre es bueno saber lo que realmente estamos haciendo en matemáticas, y concretamente con el cálculo de este tipo de operaciones que más o menos todos sabemos resolver al menos sus casos más esenciales, este hecho no ocurre siempre, y al final se acaban resolviendo de forma mecánica y sin ser conscientes de muchas de sus verdaderas utilidades.